Wszystko - Twierdzenie Talesa

Twierdzenie Talesa – jedno z najważniejszych twierdzeń całej geometrii euklidesowej. Tradycja przypisuje jego sformułowanie Talesowi z Miletu.

Treść

Jeżeli ramiona kąta przecięte są prostymi równoległymi, to odcinki wyznaczone przez te proste na jednym ramieniu kąta, są proporcjonalne do odpowiednich odcinków na drugim ramieniu kąta.

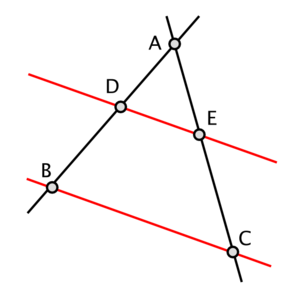
Dla powyższych rysunków zachodzi: $frac{|AD|}{|AE|}=frac{|DB|}{|EC|}=frac{|AB|}{|AC|}$

lub po przekształceniu: $frac{|AE|}{|EC|}=frac{|AD|}{|DB|}$ oraz $frac{|AE|}{|AC|}=frac{|AD|}{|AB|}$ a także $frac{|AC|}{|EC|}=frac{|AB|}{|DB|}$ .

Często spotykaną nieścisłością jest takie formułowanie twierdzenia Talesa: 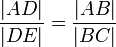$frac{|AD|}{|DE|}=frac{|AB|}{|BC|}$ , ta równość jest oczywiście prawdziwa, ale wynika z podobieństwa trójkątów ADE i ABC a nie z samego twierdzenia Talesa.

Dowód

Najstarszy zachowany dowód twierdzenia Talesa zamieszczony jest w VI. księdze Elementów Euklidesa.

Dowód oparty jest na dwóch lematach:

Jeśli dwa trójkąty mają równe wysokości, to stosunek ich pól jest równy stosunkowi długości ich podstaw.
Jeśli dwa trójkąty mają wspólną podstawę i równe wysokości, to ich pola są równe.

Dowód

Trójkąty $C E D$ i $E A D$ mają wspólną wysokość $h'$ , więc na mocy lematu 1.:

$frac{|CE|}{|EA|} = frac{[CED]}{[EAD]}$ .

Dodatkowo trójkąty $C E D$ i $B D E$ mają wspólną podstawę $E D$ i równe wysokości $h$ , dlatego na mocy lematu 2.:

[C E D] = [B D E]

, stąd $frac{[CED]}{[EAD]} = frac{[BDE]}{[EAD]}$ .

Trójkąty $B D E$ i $E A D$ mają wspólną wysokość, więc zgodnie z lematem 1:.

Przyrównując do siebie te równości otrzymuje się,

czego należało dowieść.

Komentarz

W powyższym rozumowaniu korzysta się z faktu, iż pole trójkąta liczone dla jednego boku jako podstawy i opuszczonej na niego wysokości jest równe polu liczonemu dla innego boku jako podstawy i opuszczonej na ten bok wysokości. Jest to dość silna własność funkcji pola (wyżej korzysta się z niej w drugim zdaniu dowodu), jednak nie jest ona niezbędna do dowiedzenia twierdzenia Talesa i w szkolnej matematyce cicho się ją zakłada. Notabene własność tę można udowodnić... właśnie z twierdzenia Talesa.

Aby ustrzec się błędnego koła twierdzenie Talesa można dowieść korzystając z przejścia granicznego i dobrze określonej miary (np. Lebesgue'a na płaszczyźnie): stosunkowo łatwy jest dowód, gdy $frac{|AD|}{|DB|} = frac{|AE|}{|EC|} = 1$ , podobnie gdy podzieli się odcinki w stosunku wymiernym, przypadek niewymierny dowodzi się przez przybliżenia za pomocą przejścia granicznego.

Twierdzenie odwrotne do twierdzenia Talesa

Jeżeli ramiona kąta przecięte są dwiema prostymi nie pokrywającymi się z tymi ramionami i zachodzi którykolwiek z warunków:

gdzie:

A to wierzchołek kąta
Punkty przecięcia pierwszej prostej to B (z pierwszym ramieniem) i C (z drugim ramieniem)
Punkty przecięcia drugiej prostej to D (z pierwszym ramieniem) i E (z drugim ramieniem)

to proste są równoległe.
(Jeśli zachodzi jeden z tych warunków, to drugi również)

Warunki te są spełnione dla prostych równoległych (twierdzenie Talesa) ale nie tylko dla nich. Wystarczy wyjść od prostych równoległych i odbić punkt E symetrycznie względem punktu C, a równania (1), (2) i (4) pozostaną spełnione, choć proste nie będą już równoległe. Analogicznie, po odbiciu punktu C wzlędem E, spełnione będą równania (3) i (4).

Zastosowania

Podział odcinka w danym stosunku

Dane są dwa odcinki o długościach a i b. Dany odcinek AB podzielić w stosunku a:b.

Rzut oka na rysunek i twierdzenie Talesa pozwalają stwierdzić, że punkt P dzieli odcinek w wymaganym stosunku. Powyższa konstrukcja była podstawą greckiej arytmetyki – pozwalała mnożyć i dzielić odcinki, utożsamiane przez Greków z liczbami.