Wszystko - Twierdzenie Menelaosa

Twierdzenie Menelaosa (Menelausa) – twierdzenie geometrii płaskiej pochodzące od Menelaosa z Aleksandrii, choć znane było już przed nim. Jest przydatne przy wykazywaniu współliniowości punktów (tzn. że leżą one na wspólnej prostej).

Treść

Dowolna poprzeczna wyznacza na dwóch bokach trójkąta $triangle ABC$ i przedłużeniu trzeciego boku (lub na przedłużeniach wszystkich boków) punkty $D, E, F$ w ten sposób, że iloczyn długości trzech do siebie nieprzyległych odcinków jest równy iloczynowi długości trzech pozostałych, czyli.

Zapamiętanie twierdzenia ułatwia również sztuczka mnemotechniczna polecająca kolejnym przechodzeniu od wierzchołka trójkąta (poczynając od dowolnie ustalonego) do punktu przecięcia poprzecznej na boku (przedłużeniu) zawierającym ten punkt do kolejnego wierzchołka i wróceniu w ten sposób do punktu wyjścia:

$A to E to C to D to B to F to A$ skrótowo zapisywane zwykle jako

A E C D B F A

co pomaga w zapamiętaniu, które z odcinków winny znaleźć się w liczniku, a które w mianowniku:.

Ostatnia równość jest inną postacią twierdzenia.

Dowód

Niech $X$ będzie przecięciem prostej równoległej do $A C$ przechodzącej przez punkt $B$ z poprzeczną. Trójkąty $triangle XBF$ i $triangle EAF$ są podobne. Z twierdzenia Talesa:

$frac{|BX|}{|AE|} = frac{|BF|}{|FA|}$ czyli $|XB|=frac{|BF|}{|FA|} cdot |AE|$

Trójkąty $triangle CED$ i $triangle BXD$ są podobne. Zatem jest:

$frac{|CE|}{|XB|} = frac{|DC|}{|DB|}$ czyli $frac{1}{|XB|}=frac{|DC|}{|DB|} cdot frac{1}{|CE|}$

Po pomnożeniu stronami otrzymanych równości prawdziwa jest równość

$1=frac{|BF|}{|FA|} cdot frac{|DC|}{|DB|} cdot frac{|AE|}{|CE|}$ ,

co kończy dowód. W przypadku, gdy wszystkie punkty $D, E, F$ leżą na przedłużeniach boków trójkąta, rozumowanie jest analogiczne.

Twierdzenie odwrotne

Twierdzenie odwrotne do twierdzenia Menelaosa również jest prawdziwe:

Jeżeli na bokach

A B

B C

trójkąta $triangle ABC$ dane są punkty

E

D

, a na przedłużeniu boku

A C

punkt

F

tak, że:

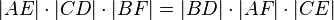$|AE| cdot |CD| cdot |BF| = |BD| cdot |AF| cdot |CE|$ ,

to punkty

D, E, F

są współliniowe.

Analogicznie, gdy wszystkie punkty $D, E, F$ leżą na przedłużeniach odpowiednich boków.

Dowód

Dowód nie wprost: niech dla pewnych niewspółliniowych punktów zachodzi

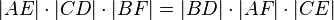$|AE| cdot |CD| cdot |BF| = |BD| cdot |AF| cdot |CE|$ (1)

oraz $D, E$ leżą na bokach trójkąta, zaś $F$ na prostej $A B$ poza bokiem.

Wtedy można wybrać taki punkt 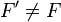$F' ne F$ , że $D, E, F'$ są współliniowe. Wtedy z twierdzenia Menelaosa zachodzi

$|AE| cdot |CD| cdot |BF'| = |BD| cdot |AF'| cdot |CE|$ .

Zatem dla dwóch różnych punktów $F, F'$ leżących na prostej $A B$ poza odcinkiem $A B$ zachodzi

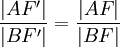$frac{|AF'|}{|BF'|}=frac{|AF|}{|BF|}$ ,

co jest sprzeczne.

Dlatego jeżeli punkty $D, E, F$ spełniają równość (1), to są współliniowe. Gdy wszystkie trzy punkty leżą poza bokami trójkąta, to dowód jest analogiczny.