Twierdzenie Napoleona – twierdzenie geometryczne orzekające, że:
ortocentra trójkątów równobocznych zbudowanych na bokach dowolnego trójkąta są wierzchołkami trójkąta równobocznego.

Tradycyjnie przypisuje się je Napoleonowi Bonaparte, choć nie ma żadnych dowodów na jego wkład w sformułowanie bądź udowodnienie twierdzenia.

Dowód 

Ponieważ trójkąty zbudowane na bokach trójkąta są równoboczne, to kąty zaznaczone na rysunku na czerwono mają miarę 30° oraz.

Stąd.

Ponieważ,

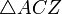więc i są podobne. Zatem

Analogicznie pokazujemy, że i są podobne, więc

Stąd | LN | = | MN | . Analogicznie pokazujemy, że | LN | = | LM | , więc jest równoboczny.